01
我有 4 位非常亲密的同事。 我们都是搞计算机的理工科之父。
我们聚在一起,建了一个微信群。
既然有了群,就必须有一个群名。
我本来想到的是“江南四大才子”这个名字,但转念一想,又想到了下面“四大才子”出现的场景:
总是感觉眼睛很痛~
人到中年了,不能再这么油腻了……
因此,朋友建议我们称这个群体为“华东五校五才俊”!
恰巧我们五个人分别来自复旦、交大、南京大学、中国科学技术大学、浙江大学,组成了华东五校的985联盟。
大家平常在群里聊的,不仅是技术,还有孩子的教育。
上周五,复旦大学的一位同事突然发来一个问题。
这个问题是他在海淀上小学四年级的侄子问的。 这是他们的数学作业。
问题如下。 给定一个正方形,需要计算阴影面积。
海淀大学四年级学生一道看似简单的数学题,竟然被我们一帮理工科的985男爸爸难住了!

大家集思广益,想了很多办法。
有人画辅助线,用全等三角形定理来求解。
有人列出方程并使用代数方程来求解它们。
有人画了辅助线,然后用相似三角形定理来解决。
虽然方法不同,最终都能得到答案,但大家都得出了相同的结论——
灾难! 太难了!
大人需要半天时间!
让一个小学四年级的孩子来做,
如何才能做到这一点?
后来我把题目给了涵涵,我向他强调这是海淀小学四年级的一道数学题。
我儿子今年上高中了。 他盯着这道小学数学题看了很久,然后睁大眼睛看着我,满是不可置信。
“爸爸,”儿子对我苦笑,“还好我没有在海淀读书,不然我可能连小学都毕业不了~”

02
昨天我见到了 SparkMath 的教学和研究负责人,这是一家总部位于新加坡的教育机构,专门教授新加坡儿童数学。
当我和他们的负责人聊天时,我忍不住谈到了我上周遇到的几何问题。
我实在不明白全等三角形教案全等三角形教案,我该如何向孩子解释清楚这个问题呢?
毕竟他们才小学四年级。 如果他们学了一堆三角形定理、一堆方程,他们根本就听不懂!
没想到这个困扰我很久的问题对于SparkMath教研老师来说却很容易。
“试试蝴蝶模型,”他微笑着给了我答案。 “新加坡数学里有一个蝴蝶模型,是专门针对这类几何题设计的,试试吧!”
蝴蝶模型? 这也是我第一次听到这个词。
但读完新加坡数学教案后,我发现这个模式太好了。
很多困扰孩子的数学问题,用了这个模型就迎刃而解了!
03
蝴蝶模型很有趣,它有两个层次。
我们先说第一层,这是蝴蝶模型的基础。
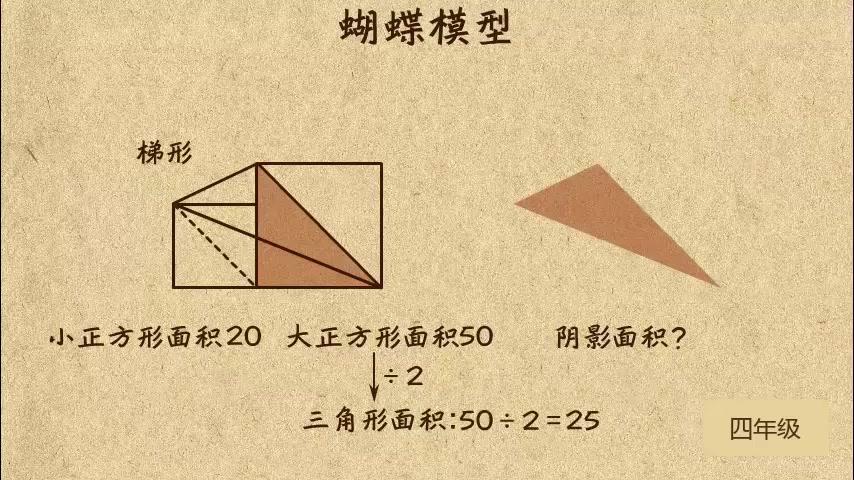
例如下图中,ABCD是梯形。
里面有两个三角形,左边是蓝色三角形,右边是红色三角形。

我们可以得出结论:
蓝色三角形和红色三角形的面积相等!
更进一步,因为两个三角形都有一个共同的紫色三角形。
因此我们还可以得出一个新的结论:
下图中,S2对应的蓝色三角形和S4对应的红色三角形面积相等!
你认为红色和蓝色的三角形看起来像蝴蝶的两个翅膀吗?
因此这个图形被称为“蝴蝶模型”!
这个模型很容易理解,但很容易使用!
有很多数学问题让我们成年人似乎不知所措。 如果我们使用这个蝴蝶模型,我们可以在几秒钟内理解它们!
例如这个问题:
左右两边都是正方形。 右边正方形的边长是8,红色三角形的面积是多少?
看来你没有任何线索,对吧? 我们可以使用蝴蝶模型!
首先画一条红线。
这样ACEG就是一个梯形,我们得到两个三角形。
其一是下面的红色三角形:
另一种是下面的蓝色三角形:
根据“蝴蝶模型”,这两个三角形的面积相等。
因此,我们只需要计算蓝色三角形的面积就可以得到红色三角形的面积。
答案是32,是不是超级简单!
04
你看,只要孩子掌握了“蝴蝶模型”,看似极其复杂、无从下手的问题,通过三角形的类比就能轻松解决。
但上面所说的只是“蝴蝶模型”的第一层。 很多人不知道的是,它还有第二层。
还是看前面的梯形,假设AD的长度为a,BC的长度为b,红色和蓝色三角形的高度分别为h1和h2。
因为红色和蓝色三角形是相似三角形。
所以我们可以得到以下结论:
回到问题的开头:
我们可以计算出梯形AMCB的面积:
因此,根据“蝴蝶模型”的公式,我们可以得到以下答案。
05
了解了新加坡数学的“蝴蝶模型”后,我真的很感动。
本来我们这些男性科学与工程之父们都在摸着石头过河,想尽办法去解决这个问题,没想到用蝴蝶模型就能轻松解决。
说白了,蝴蝶模型的本质就是把复杂的事情简单化,进行图形类比,把一个复杂的图形和一个简单的图形进行比较,这样就可以很容易得到答案。
小学数学从三年级开始就陆续出现了几何题,而且有些题还相当复杂。
当孩子遇到复杂的几何题时,不要做计算,不要过度,看看能不能换个图形,做个图形类比,这样就能找到简单的解法!
而我今天讲的新加坡数学的“蝴蝶模型”就是一个非常好的方法!
希望对孩子们的数学有所帮助!
新加坡数学的特点是用大量的图形来展示。 方法非常灵活巧妙,也给了我很多参考和启发。
